This is a quick guide to using Expendable for modelling home finances. If you want to be able to predict how much time or interest can be saved on a mortgage by using an offset facility, or want to see the effects of using a cash ISA or regular saver account, or any other type of savings account, this might be for you.
Start off by installing it. On Fedora 9 you can do this by selecting System → Administration → Add/Remove Software from the menu and searching for “expendable”. If you are using Fedora 8, select Applications → Add/Remove Software.
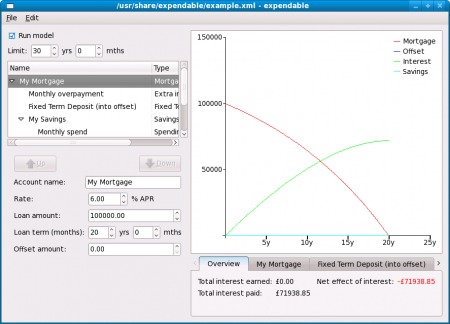
After installing it, you can run the program by selecting Applications → Office → Expendable from the main menu. You should see something like this (click for a close-up):
A straightforward mortgage
This example data shows how the program can be used straight away. Let’s say we have a mortgage with Nationwide, with an outstanding balance of £80,500 and 12 years 3 months left to run. (These figures will be on your most recent mortgage statement.)
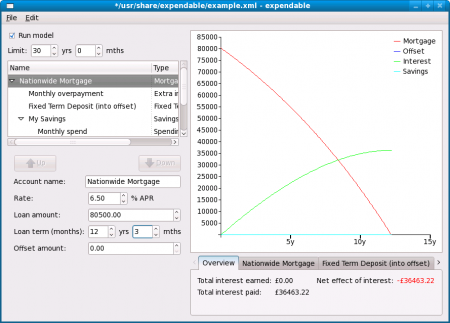
Click on ‘My Mortgage’ in the account name field on the left hand side, about half-way down the screen, and replace that text with “Nationwide Mortgage”. Let’s say the interest rate is 6.5% APR: use the up-arrow button next to the interest rate field to set that. You’ll notice the graph changing as you do this. Now adjust the loan amount to £80,500 (you’ll have to type in “80500”, as the up/down arrows make changes in increments of £1,000). Now use the arrow buttons on the next line down to adjust the term to 12 years and 3 months. Your window should now look like this:
As you can see, the graph has been updated to reflect the details we just entered. The horizontal axis shows time moving forward, with 5-year intervals marked. The red line shows the outstanding mortgage balance over time, decreasing more quickly when the loan is nearly repaid. The green line shows the total amount of interest paid.
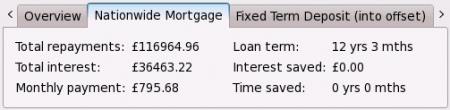
Below the graph are some figures illustrating this. The “overview” part shows the total amount of interest paid. Click on the “Nationwide Mortgage” part to see more details about the mortgage:
Using an offset facility
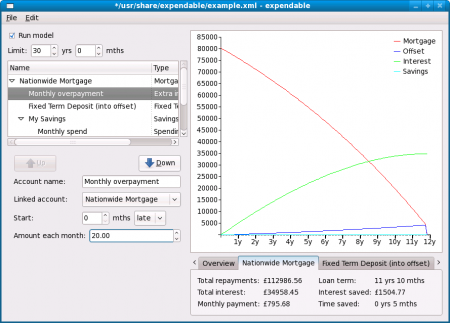
So much for the mortgage; now let’s try something interesting. We can find out the effect on the mortgage if we are able to overpay each month by, say, £20. To do this, click on ‘Monthly overpayment’ in the box on the left hand side. Below the box, adjust the ‘amount each month’ field to 20. Now there is a blue line on the graph, and this illustrates the amount in the offset facility of the mortgage.
Paying an extra £20 each month into a mortgage that has an offset facility increases the amount in the offset by that much. It is effectively a savings account, but rather than paying interest on the amount in the offset account, the amount of interest charged on the mortgage is reduced as though the loan amount were smaller.
As you can see, the loan term has now shortened by 5 months, to 11 years and 10 months. This is a saving in mortgage interest of over £1,500. When the blue line (the offset account) hits the red line (the outstanding loan amount), they both drop to zero — at that point, the loan has been repaid.
You can save this model by selecting File → Save As… from the menu.
Savings account with fixed term deposit
Now let’s try an example using a savings account as the main focus. This time, we have £10,000 in a savings account paying 6.5% AER, but we want to put half of it into a high-interest fixed term deposit. The FTD pays 10% AER but locks away the money for a year.
To set this up, select File → New from the menu, choose Savings Account, and click OK.
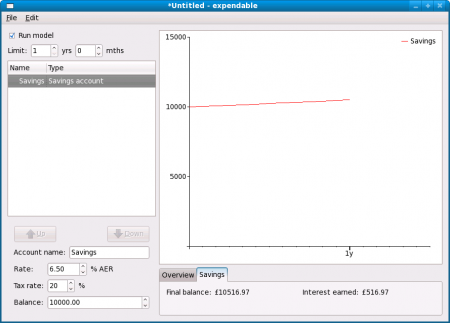
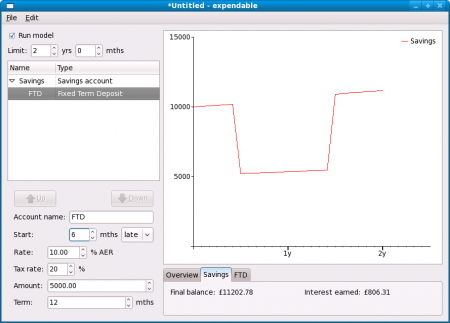
Name this account “Savings” and set the rate and balance. Leave the tax rate at 20% — this means that our savings interest is taxed at the basic rate. The graph is drawn showing an ever-increasing balance. By default, the first 30 years are modelled, and for this example we only want to see the first year. Adjust the ‘Limit’ fields at the top left of the window, below the ‘Run model’ checkbox, to “1 yrs 0 mths”. Notice that below the graph, the final balance of the savings account is shown in the “Savings” tab: £10,516.97.
Now we want to add a fixed term deposit. Select Edit → Add Account from the menu and choose Fixed Term Deposit, then click OK.
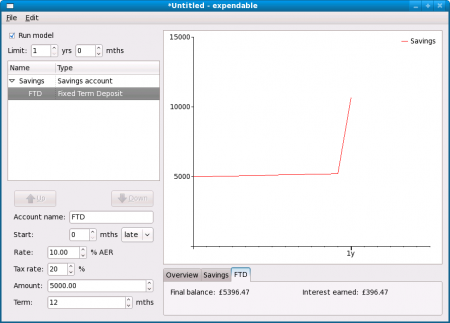
Name this account “FTD” and set the rate to 10. Now adjust the amount up to 5000. The final balance in the savings account after 1 year is now shown as £10,677.67, and by flipping between the “Savings” and “FTD” tabs below the graph we can see that this is due to £281.20 in interest from the savings account and £396.47 from the fixed term deposit.
This example shows a bit more about how the accounts tree works. The fixed term deposit account takes its initial balance from its “parent” account, the savings account. When the term is up, it pays back into its parent account. This sort of thing works for mortgages too. You can set up quite complicated arrangements if you wish, for example a mortgage which will be paid off by a savings account, which in turn has several linked fixed term deposits. The example data file shown when you first start the program gives a good starting point for experimentation.
You can also use this example to see the effect of waiting 6 months before setting up the fixed term deposit, as follows. First, increase the limit to 2 years. Next, find the “Start: 0 mths late” part and adjust it to “6 mths late”.
Savings account with regular saver
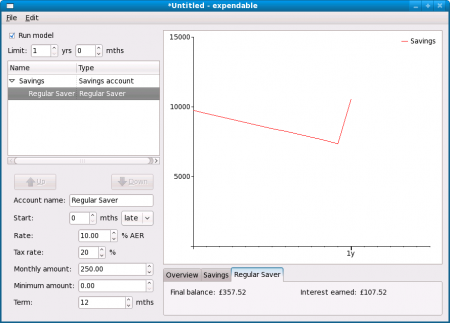
Here’s another example using a savings account. In this case, we’ll be “drip-feeding” a regular saver account from a savings account. A regular saver account is similar to a fixed term deposit, but rather than setting it up from one lump sum at the beginning, monthly contributions are made. Typically these last for a year and the maximum monthly contribution is £250. The money is locked away for that time. For our example, the savings account pays 6.5% AER, we have £10,000 in it, and the regular saver pays 10% AER and we want to pay £250 into it each month.
Martin Lewis’s web site has a calculator for modelling just this type of situation.
So, here’s how we’ll set it up: first, select File → New from the menu and choose to create a savings account. Give it a name, and set the rate to 6.5 and balance to 10000. Now select Edit → Add Account and add in a Regular Saver. Give that a name and set the rate to 10, and the monthly amount to 250. Set the limit to 1 year to see the result: the total interest earned in the first year is £542.44, with £434.92 of that coming from the normal savings account and £107.52 from the regular saver.
Using up savings
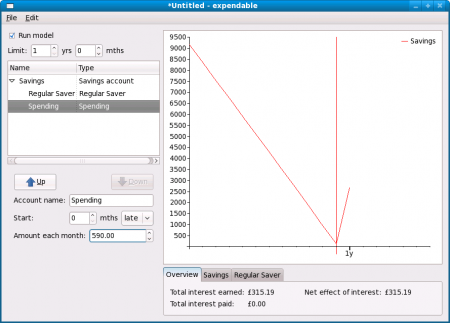
Finally, let’s try an example in which we have savings, but are spending them. The questions we need to know the answers to are: how much can we overspend by each month, and how long can that last before the savings run out?
We’ll use the same data as in the previous example, but we’d better make sure we set the “minimum amount” for the regular saver. If there is not enough money to contribute the monthly amount (£250), the minimum amount will be contributed. Let’s say that in this example, there is no flexibility at all: the minimum is £250 as well.
To simulate spending with abandon, add another account, this time of type “spending”. Now, click on the up-arrow next to “amount each month” until the amount stops changing.
A vertical line is drawn at the point in time where spending any more each month will result in the savings running out: 11 months from now, if the monthly shortfall is £590.
Feedback please!
There are lots of ways of combining different account models, and lots of different types of questions that can be answered by using this modelling program. If you have a problem getting it to behave the way you want it to, or have an idea for making it better, please let me know by adding a comment below.

Comments
3 responses to “Expendable tutorial (offset mortgage calculator)”
[…] expendable can make calculations for stoozing as well. Stoozing, if you haven’t heard that word, is […]
When using the mortgage calculations, it would be nice to model the “real” percentages: 4.375 versus 4.37 or 4..38
I’ve upped it from 2 decimal places to 4 — does that help?